Last Updated on December 13, 2025 by Admin
Notes
- The Black-Scholes-Merton Model is a mathematical formula used to derive the estimated fair price of a Call or Put Option
The model was published by;
- Fischer S. Black, Sloan School of Management, Massachusetts Institute of Technology (MIT)
- Myron S. Scholes, Booth School of Business, University of Chicago
- Paper: “The Pricing of Options and Corporate Liabilities”
- Journal: Journal of Political Economy, Vol. 81, No. 3 (May – Jun., 1973), pp. 637-654
- Publisher: University of Chicago Press
- Publication Date: May 1973
- Significance: This is the original paper introducing the Black-Scholes model, providing a formula for pricing European options based on no-arbitrage principles and continuous-time finance.
Note: When the Black-Scholes paper “The Pricing of Options and Corporate Liabilities” was published in 1973, Fischer Black was listed as being affiliated with the University of Chicago, while Myron Scholes was listed with the Massachusetts Institute of Technology (MIT) Sloan School of Management. This appears reversed because, although much of the research was done while Black was at MIT and Scholes at Chicago, the paper reflected their institutional affiliations at the time of publication, not during the research process.
The model was extended and published by;
- Robert C. Merton, Sloan School of Management, Massachusetts Institute of Technology (MIT)
- Paper: “Theory of Rational Option Pricing”
- Journal: The Bell Journal of Economics and Management Science
- Publisher: The RAND Corporation
- Publication Date: Spring 1973
- Significance: This paper extended and generalised the Black-Scholes framework, provided a more rigorous mathematical derivation, and showed how it could be applied to a wide range of contingent claims giving rise to the Black-Scholes-Merton model.
Assumptions
- Risk-Free Benchmark: The Black–Scholes–Merton model assumes there is a risk-free asset, such as government treasury bills, which serves as a reference point for evaluating the performance of a risky asset.
- No Dividend Payments: It is assumed that the underlying asset does not distribute dividends or other income during the life of the option.
- Random Price Movements: Asset prices are assumed to follow a random walk, meaning they move unpredictably, and past movements do not influence future changes.
- Unlimited Market Access: Investors are free to buy or sell any quantity of the asset without restrictions on trade size or volume.
- No Transaction Costs: The model assumes frictionless markets with no brokerage fees, commissions, or other transaction costs affecting trading or pricing.
- Constant Volatility: The volatility of the underlying asset, a measure of how much its price fluctuates is assumed to remain constant over the life of the option.
Key Formulas
Call Option
$$C=SN(d_{1})-Ke^{-rT}N(d_{2})$$
Put Option
$$P=Ke^{-rT}N\left(-d_{2}\right)-SN\left(-d_{1}\right)$$
$$d_{1}=\frac{ln\frac{S}{K}+\left( r+\frac{\sigma^{2}}{2} \right)T}{\sigma\sqrt{T}}$$
$$d_{2}=d_{1}-\sigma\sqrt{T}$$
The Greeks
Delta (Δ): Measures the change in the value of the option with respect to the change in the price of the underlying asset.
$$Δ_{Call}=N(d1)$$
$$Δ_{Put}=N(d1)-1$$
Gamma (Γ): Measures the rate of change in an option’s delta for every $1 move in the underlying asset’s price.
$$Γ=\frac{N′(d1)}{Sσ\sqrt{T}}$$
Theta (Θ): Measures the rate of time decay, which is the amount an option’s value is expected to decrease each day as it gets closer to its expiration date.
$$Θ_{Call}=\frac{SN'(d1)σ}{2\sqrt{T}}−rKe^{−rT}N(d2)$$
$$Θ_{Put}=\frac{SN'(d1)σ}{2\sqrt{T}}+rKe^{−rT}N(-d2)$$
Vega (ν): Vega measures the sensitivity of an option’s price to changes in the volatility of the underlying asset. More specifically, it represents the change of an option’s price for a 1% change in implied volatility all else being equal. Vega is always going to be positive for both Calls and Puts.
$$ν=SN'(d1)\sqrt{T}$$
Note: The Probability Density Function (PDF) is the first derivative of the Cumulative Distribution Function (CDF)
i.e. N(d1) -> N'(d1)
Rho (ρ): Measures the expected change in an option’s price for every 1% change in interest rates.
$$ρ_{Call}=KTe^{−rT}N(d2)$$
$$ρ_{Put}=-KTe^{−rT}N(-d2)$$
Variables
- C = Call Option Price
- P = Put Option Price
- S = Spot Price of the Underlying Asset
- K = Strike (Exercise) Price of the Option
- e = Euler’s Number (Base of Natural Logarithm)
- r = Risk-Free Interest Rate
= Volatility
- T = Time to Maturity (Expiration)
- N(·) = Cumulative Distribution Function (CDF)
- N'(·) = Probability Density Function (PDF)
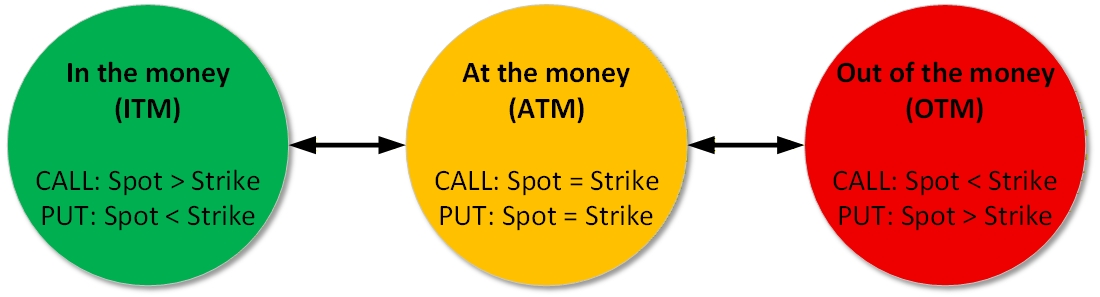
Moneyness
Measures how profitable an option would be if exercised immediately.
Black-Scholes-Merton (BSM) Calculator
